Hard days but Magic Knights for CQU Academic
Published on 06 February, 2003
A small piece of history has been made in regard to magic knight\\\'s tours by a Central Queensland University academic, Tim Roberts.
Mr Roberts recently discovered two new magic knight’s tours, the first new tours to be found since 1988, and the first irregular tours found since 1936.
“Magic knight’s tours fall under a part of discrete mathematics known as graph theory, with the tour itself being a Hamiltonian,” Mr Roberts explains. “But you don’t need to understand any advanced maths to understand the concepts involved – they’re very simple.
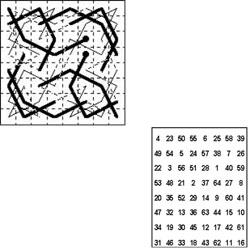
“A magic square is one in which the numbers in all of the rows and columns add up to the same total. A knight’s tour is a tour of the board in which every square is visited exactly once using the knight’s move in chess. A magic knight’s tour just combines these two elements.
Though work has been done on boards of all different dimensions, the classic problem relates to the standard eight by eight board. Almost all magic knight’s tours on such a board are regular tours – they conform to a pattern where every group of four moves is confined to a single quadrant of the board.
A quarte is any segment of four cells in an arithmetical tour that are numbered 4x+1 to 4x+4 for some value x. A regular quarte is a quarte confined to a single quadrant and with the special property that it uses one cell on each row and one cell on each column of the quad. Three types are possible: a square or a diamond or a beverley quarte.
In a regular tour all the quartes are regular and each quadrant therefore contains four quartes.
The last regular tours were found by Tom Marlow in 1988. Irregular tours – that is, tours which use irregular quartes - are much harder to find.
Until Tim’s discovery of two new irregular tours in January this year, H J R Murray founded the last ones back in 1936.
“Application? Probably none”, said Tim, “but for many years most number theories were thought to be quite useless too, and then it suddenly assumed enormous importance in the field of cryptography. As to the future, who knows.
Above: The first of the two new tours, designated Roberts 2003 01i; in the geometrical diagram below, the irregular quartes are shown in bold: Left: Central Queensland University lecturer Tim Roberts has discovered a new mathematical theory.